Přístupy (strategie) návrhu

algoritmu

Návrh algoritmu představuje klíčovou disciplínu informatiky a teoretické počítačové vědy. Cílem není pouze vytvořit funkční postup řešení, ale také zajistit jeho efektivitu, optimalitu a škálovatelnost. V praxi se pro konstrukci algoritmů využívají různé strategické přístupy (design paradigms), které určují způsob, jakým se problém rozkládá a řeší. Mezi nejvýznamnější čtyři přístupy patří:

1. Rozděl a panuj (Divide and Conquer)

2. Dynamické programování (Dynamic Programming)

3. Hladový algoritmus (Greedy Algorithm)

4. Hrubá síla (Brute Force)

Tyto strategie se uplatňují napříč obory od řazení a vyhledávání, přes grafové úlohy, až po optimalizační a kombinatorické problémy.

Rozděl a panuj (Divide and Conquer)

Princip

Strategie rozděl a panuj spočívá v rozložení složitého problému na menší, jednodušší podproblémy, které jsou rekurzivně řešeny a jejich výsledky jsou následně kombinovány do celkového řešení.

Tento přístup se dá formálně popsat ve třech krocích:

1. Rozdělení (Divide): Problém se rozdělí na menší podproblémy stejného typu.

2. Ovládnutí (Conquer): Každý podproblém se řeší samostatně (rekurzivně).

3. Sjednocení (Combine): Výsledky podproblémů se spojí do celkového řešení.

Typické příklady

Merge Sort (řazení slučováním)

Quick Sort (rychlé řazení)

Binary Search (binární vyhledávání)

Fast Fourier Transform (FFT)

Charakteristika

Tento přístup je efektivní zejména tam, kde lze problém přirozeně dělit a kde rekurzivní řešení výrazně zkracuje časovou složitost oproti přímému postupu.

Dynamické programování (Dynamic Programming)

Princip

Dynamické programování využívá princip optimalizace s pamětí – problém je rozložen na menší podproblémy, které se však často překrývají. Místo jejich opakovaného řešení jsou výsledky ukládány do tabulky (tzv. memoizace) a znovu použity.

Tento přístup je vhodný, pokud platí dvě klíčové vlastnosti:

Optimální podstruktura – optimální řešení celku lze složit z optimálních řešení podproblémů.

Překrývající se podproblémy – stejné dílčí úlohy se objevují vícekrát.

Typické příklady

Fibonacciho posloupnost (tabulkový výpočet)

Problém batohu (Knapsack problem)

Nejkratší cesta v grafu (Dijkstra, Floyd-Warshall)

Úprava řetězců (Edit Distance, DNA alignment)

Charakteristika

Dynamické programování přináší často exponenciální zrychlení oproti hrubé síle. Je však náročnější na paměť, protože vyžaduje ukládání mezivýsledků.

Hladový algoritmus (Greedy Algorithm)

Princip

Hladový (Greedy) přístup vybírá v každém kroku lokálně nejlepší možné řešení s nadějí, že z těchto lokálních voleb vznikne řešení globálně optimální.

Neprovádí zpětné kroky ani neuchovává historii rozhodnutí – volí vždy „nejlepší“ variantu tady a teď.

Typické příklady

Kruskalův a Primův algoritmus pro minimální kostru grafu

Dijkstrův algoritmus pro nejkratší cesty

Huffmanovo kódování (komprese dat)

Problém výběru aktivit (Activity Selection Problem)

Charakteristika

Hladové algoritmy jsou rychlé a jednoduché, ale ne vždy zaručují globálně optimální výsledek. V praxi se často využívají pro aproximace nebo heuristické řešení složitých úloh.

Hrubá síla (Brute Force)

Princip

Strategie hrubé síly znamená systematické vyzkoušení všech možných řešení a výběr nejlepšího. Je to nejjednodušší, ale i nejméně efektivní přístup.

Používá se, pokud není znám lepší algoritmus nebo pro ověření správnosti jiných metod.

Typické příklady

Problém obchodního cestujícího (TSP) – vyzkoušení všech permutací

Vyhledávání vzoru v textu (naivní algoritmus)

Kombinatorické úlohy (permutace, kombinace, uspořádání)

Charakteristika

Hrubá síla je výpočetně náročná (obvykle exponenciální časová složitost), avšak jistě nalezne optimální řešení. Slouží jako referenční nebo výukový přístup při analýze složitějších algoritmů.

Srovnání strategií

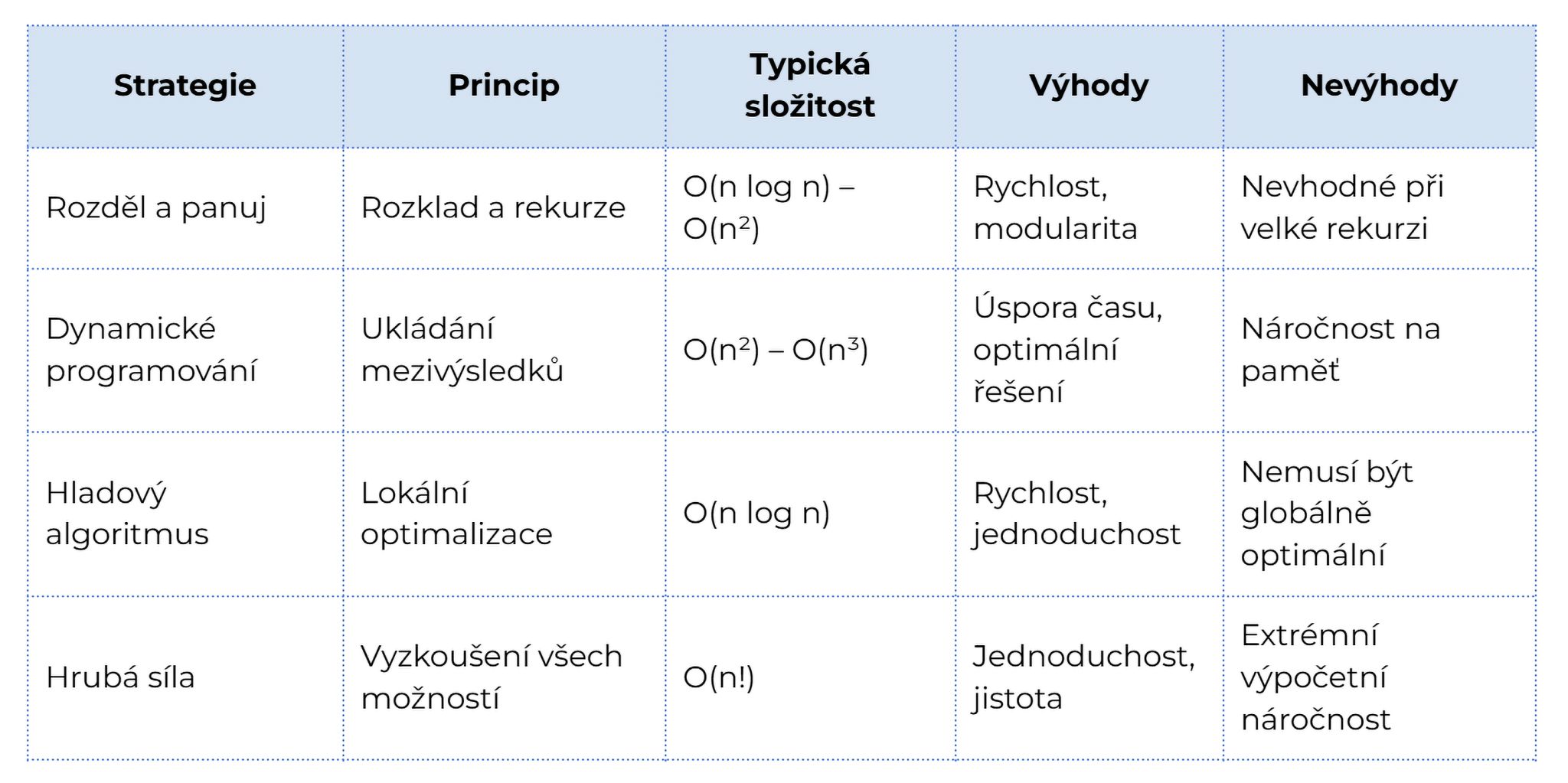
Strategie návrhu algoritmu jsou základním kamenem efektivního řešení problémů v informatice. Zatímco hrubá síla je jednoduchá, ale pomalá, přístupy jako rozděl a panuj nebo dynamické programování dokážou problémy řešit s výraznou efektivitou. Hladové algoritmy pak nabízejí kompromis mezi rychlostí a kvalitou výsledku.

Porozumění těmto paradigmatům je nezbytné nejen pro studenty programování, ale i pro každého, kdo se zabývá vývojem softwaru, optimalizací procesů nebo umělou inteligencí.